渐进DID估计量的分解及偏误来源 链接到标题
dCDH 分解 链接到标题
dCDH (2020, AER) 指出,在平行趋势成立的情况下,渐进DID的估计参数$\beta_{fe}$是所有处理$(g,t)$格的加权平均 $$\beta_{fe} = E \left( \sum_{(g,t): D_{g,t} = 1} w_{g,t} \Delta_{g,t} \right). $$
- 这里 $\Delta_{g,t}$ 是分组 $g$ 在时间 $t$ 的平均处理效应ATE;
- $w_{g,t}$为权重,其和为1,但是可能取负值。这里对负值的解释与 Goodman-Bacon (2021, JoE)类似 当权重存在负值时,即使所有$\Delta_{g,t}$都为正,$\beta_{fe}$也可能为负。
Goodman-Bacon 分解 链接到标题
Goodman-Bacon (2021, JoE) 将 DID 参数分解为多个双重差分的加权平均,如果处理效应随着时间变化,即使平行趋势假设成立,估计量也会偏离我们想要的ATT。下面我们根据一个简单的设定进行说明:
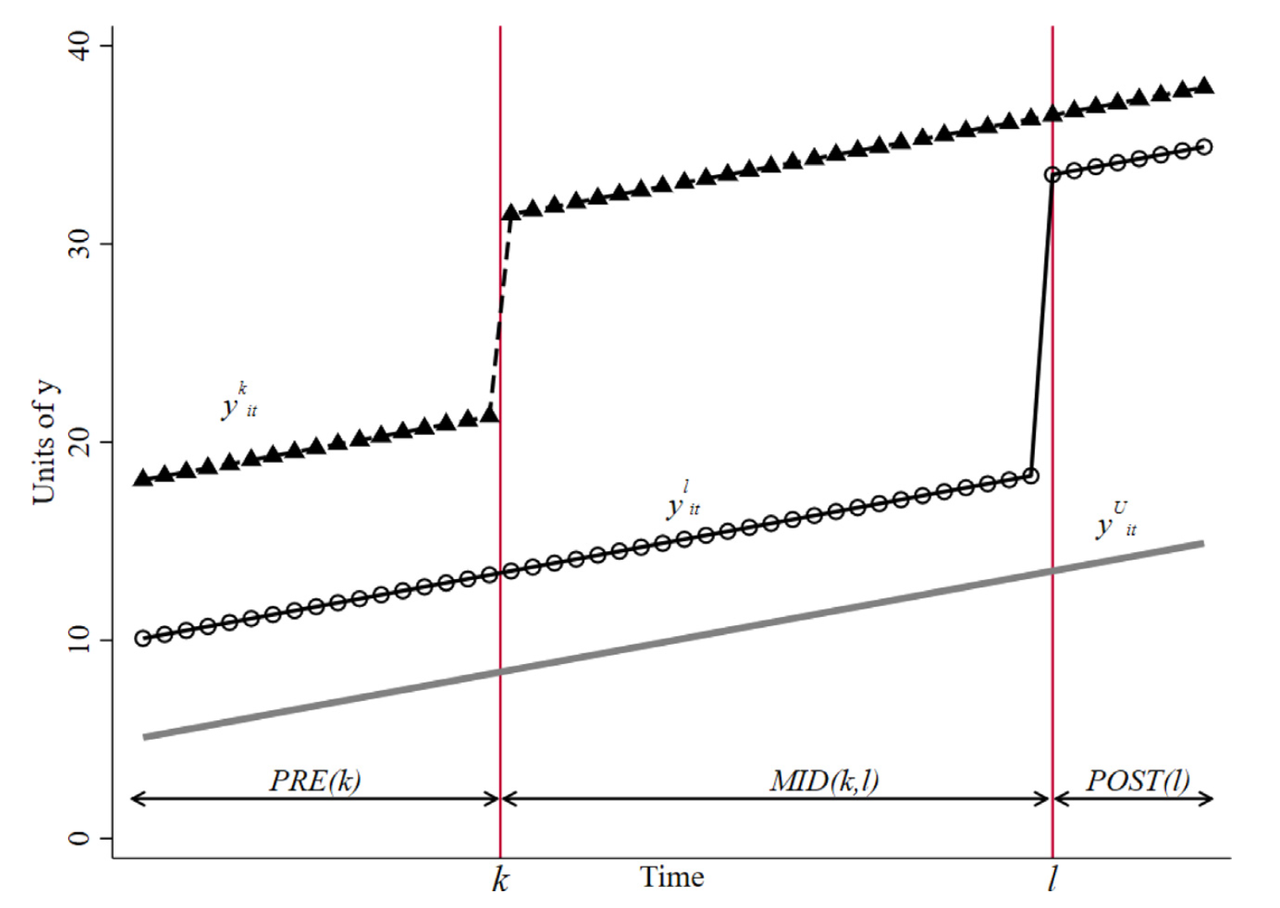
如上图,处理组分为两类,处理组$k$和处理组$l$,其中$k$早受处理,处理时间为 $t_k$,而$l$晚受处理,处理时间$t_l$。这里时间分为三段:
- $PRE(k)$:$k$未受处理,$l$未受处理
- $MID(k,l)$: $k$受处理,$l$未受处理
- $POST(l)$: $k$受处理,$l$受处理
如果通过TWFE模型进行回归 $$y_{it} = \alpha_i + \alpha_t + \beta^{DD}D_{it} + e_{it}$$ 那么估计系数$\hat{\beta}^{DD}$可以分解为以下四个部分:
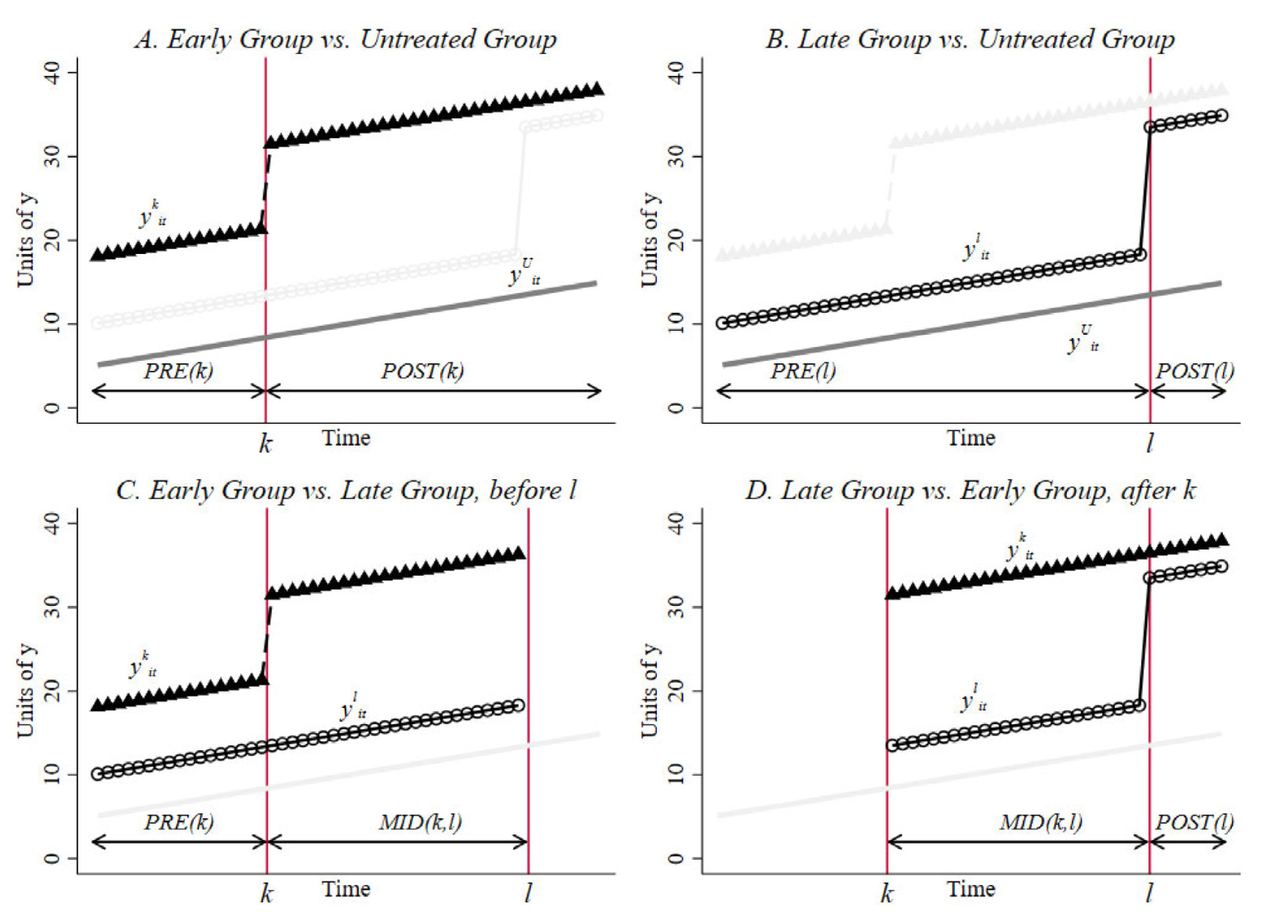
- 早处理组与非处理组对比(Panel A),其TWFE的估计系数为 $$\hat{\beta}_{kU}^{2\times2} \equiv \left( \bar{y}_k^{POST(k)} - \bar{y}_k^{PRE(k)} \right) - \left( \bar{y}_U^{POST(k)} - \bar{y}_U^{PRE(k)} \right)$$
- 晚处理组与非处理组对比(Panel B) $$\hat{\beta}_{jU}^{2\times2} \equiv \left( \bar{y}_j^{POST(j)} - \bar{y}_j^{PRE(j)} \right) - \left( \bar{y}_U^{POST(j)} - \bar{y}_U^{PRE(j)} \right)$$
- 早处理组与晚处理组未受处理时对比(Panel C)$$\hat{\beta}_{kl}^{2\times2,k} \equiv \left( \bar{y}_k^{MID(k,l)} - \bar{y}_k^{PRE(k)} \right) - \left( \bar{y}_l^{MID(k,l)} - \bar{y}_l^{PRE(k)} \right)$$
- 晚处理组与早处理组对比(Panel D)
$$\hat{\beta}_{kl}^{2\times 2,l} \equiv \left( \bar{y}_l^{POST(l)} - \bar{y}_l^{MID(k,l)} \right) - \left( \bar{y}_k^{POST(l)} - \bar{y}_k^{MID(k,l)} \right)$$
具体而言,$\hat{\beta}^{DD}$ 可以表示为以上估计参数的加权平均 $$ \hat{\beta}^{DD}=\sum_{k\neq U} s_{kU} \hat{\beta}_{kU}^{2\times 2}+ \sum_{k \neq U}\sum_{l > k}\left[s_{kl}^k \hat{\beta}_{kl}^{2 \times 2, k}+s_{kl}^l \hat{\beta}_{kl}^{2 \times 2, l}\right] $$ 这里的权重 $s$ 与对应子样本的规模大小和处理变量(经固定效应调整后)的方差相关,这个方差受处理组和控制组的相对大小和受处理的时间相关
- 两组大小相近($n_{kU} \approx 0.5$),方差越大
- 受处理的时间越居中,方差越大
更一般地,双向固定效应双重差分估计量的概率极限可以分解为(具体推导省略)三个部分
$$\plim_{N\to \infty} \hat{\beta}^{DD} = \beta^{DD} = \text{VWATT} + \text{VWCT} - \Delta\text{ATT}$$
这里 VWATT 为 variance-weighted average treatment effect on the treated,第二项为 variance-weighted common trends, 第三项为 change in treatment effects within each timing group’s before and after a later treatment time。
如果处理效应随着时间变化,那么$\Delta ATT$不为零,即使平行趋势假设不违背,估计量也会偏离VWATT。
什么时候渐进DID存在偏误 链接到标题
Baker et al. (2022) 对以上文献进行总结,从理论和直观上解释了渐进DID的问题,基本上存在动态效应的时候,渐进DID的结果有偏。
- 多时点 DID 中,早受处理的个体会作为后处理个体的控制组。引发坏比较(bad comparision) 问题
- 即使随机实验,渐进DID仍然可能获得相反的估计系数符号。
- 动态处理效应存在的情况下,静态DID仍然无偏
- 同质处理效应(时间和企业层面)情况下,渐进DID是无偏的
- 异质性处理效应下,渐进DID是有偏的
- 事件分析在动态效应方面也存在问题 (Sun and Abraham, 2021)
怎么处理 链接到标题
TODO
参考文献 链接到标题
Baker, Andrew C., David F. Larcker, and Charles C. Y. Wang. 2022. “How Much Should We Trust Staggered Difference-in-Differences Estimates?” Journal of Financial Economics 144 (2): 370–95. https://doi.org/10.1016/j.jfineco.2022.01.004.
Callaway, Brantly, and Pedro H.C. Sant’Anna. 2021. “Difference-in-Differences with Multiple Time Periods.” Journal of Econometrics 225 (2): 200–230. https://doi.org/10.1016/j.jeconom.2020.12.001.
Chaisemartin, Clément de, and Xavier D’Haultfœuille. 2020. “Two-Way Fixed Effects Estimators with Heterogeneous Treatment Effects.” American Economic Review 110 (9): 2964–96. https://doi.org/10.1257/aer.20181169.
Goodman-Bacon, Andrew. 2021. “Difference-in-Differences with Variation in Treatment Timing.” Journal of Econometrics, Themed Issue: Treatment Effect 1, 225 (2): 254–77. https://doi.org/10.1016/j.jeconom.2021.03.014.